Earthquake Resistant Buildings Design

Seismic effects on the structure

Earthquake causes shaking of the ground. So a building resting on it will experience motion at its base. From Newton's First Law of Motion, even though the base of the building moves with the ground, the roof has a tendency to stay in its original position. But since the walls and columns are connected to it, they drag the roof along with them. This tendency to continue to remain in the previous position is known as inertia. In the building, since the walls or columns are flexible, the motion of the roof is different from that of the ground (Figure 1).

Buildings experience motion due to earthquake.

Effect of Deformations in Structures

The inertia force experienced by the roof is transferred to the ground via the columns, causing forces in columns.

• During earthquake shaking, the columns undergo relative movement between their ends.

• 

  In Figure 2, this movement is shown as quantity u between the roof and the ground.
• The larger is the relative horizontal displacement u between the top and bottom of the column, the larger this internal force in columns.
• Also, the stiffer the columns are (i.e., bigger is the column size), larger is this force.
• For this reason, these internal forces in the columns are called stiffness forces. In fact, the stiffness force in a column is the column stiffness times the relative displacement between its ends.

Horizontal and Vertical Shaking

• Earthquake causes shaking of the ground in all three directions - along the two horizontal directions (X and Y, say), and the vertical direction (Z, say) (Figure 3).
• All structures are primarily designed to carry the gravity loads, The downward force Mg is called the gravity load.
• The vertical acceleration during ground shaking either adds to or subtracts from the acceleration due to gravity.
• Since factors of safety are used in the design of structures to resist the gravity loads, usually most structures tend to be adequate against vertical shaking.
• However, horizontal shaking along X and Y directions (both + and - directions of each) remains a concern.
• Structures designed for gravity loads, in general, may not be able to safely sustain the effects of horizontal earthquake shaking. Hence, it is necessary to ensure adequacy of the structures against horizontal earthquake effects.

Flow of Inertia Forces to Foundations

• Under horizontal shaking of the ground, horizontal inertia forces are generated at level of the mass of the structure (usually situated at the floor levels).
• These lateral inertia forces are transferred by the floor slab to the walls or columns, to the foundations, and finally to the soil system underneath (Figure 4).
• So, each of these structural elements (floor slabs, walls, columns, and foundations) and the connections between them must be designed to safely transfer these inertia forces through them.
• Walls or columns are the most critical elements in transferring the inertia forces.
• But, in traditional construction, floor slabs and beams receive more care and attention during design and construction, than walls and columns.
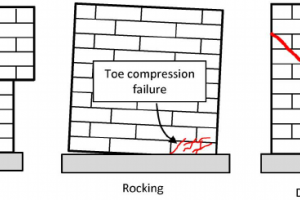
• Walls are relatively thin and often made of brittle material like masonry.
• Similarly, poorly designed and constructed reinforced concrete columns can be disastrous.

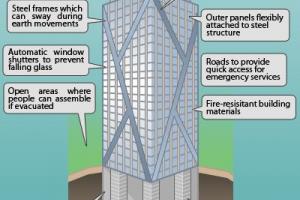
How Architectural Features Affect Buildings During Earthquakes?

Importance of Architectural Features

• The behavior of a building during earthquakes depends critically on its overall shape, size and geometry, in addition to how the earthquake forces are carried to the ground.
• Hence, at the planning stage itself, architects and structural engineers must work together to ensure that the unfavorable features are avoided and a good building configuration is chosen.

Other undesirable scenarios

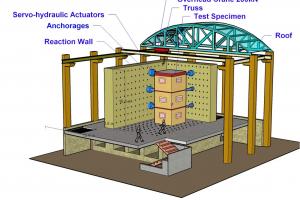
Earthquake Design Philosophy

Gravity vs Earthquake Loading in a Reinforced Concrete Building

• Reversal of stresses takes place during earthquake shaking
• Gravity loads (Self-weight) cause RC frames to bend, resulting in stretching and shortening at various locations. Tension is generated on surfaces

ACI special provisions for seismic design

General

• The principal goal of the Special Provisions is to ensure adequate toughness under inelastic displacement reversals brought on by earthquake loading.

• The provisions accomplish this goal by requiring the designer to provide for concrete confinement and inelastic rotation capacity.

• No special requirements are placed on structures subjected to low or no seismic risk.

• Structural systems designed for high and moderate seismic risk are referred to as Special and Intermediate respectively.

Concrete and Steel strength

• To ensure adequate ductility and toughness under inelastic rotation, ACI Code 21.2.4 sets a minimum concrete strength of 3000 psi.

• For lightweight aggregate concrete, an upper limit of 5000 psi is placed on concrete strength; this limit is based on a lack of experimental evidence for higher-strength lightweight concretes.

• The ACI Code 21.2.5 allows the use of Grades 40 and 60 reinforcement meeting the requirements of ASTM A615, provided that the actual yield strength does not exceed the specified yield by more than 18 ksi and that the actual tensile strength exceeds the actual yield strength by at least 25 percent.

Hoops, ties and cross ties

• Confinement for concrete is provided by transverse reinforcement consisting of stirrups. hoops, and crossties.

• To ensure adequate anchorage, a seismic hook [with a bend not less than 135° and a 6 bar diameter (but not less than 3 in.) extension that engages the longitudinal reinforcement and projects into the interior of the stirrup or hoop] is used on stirrups, hoops and cross-ties.

• Hoops are closed ties that can be made up of several reinforcing elements, each having seismic hooks at both ends, or continuously wound ties with seismic hooks at both ends.

• A crosstie is a continuous reinforcing bar with a seismic hook at one end and a hook with not less than a 90° bend and at least a 6 bar diameter extension at the other end. The hooks on crossties must engage peripheral longitudinal reinforcing bars.

Hoops, ties and crossties: Advantages

Closely spaced horizontal closed ties in Column help in three ways, namely

1. they carry the horizontal shear forces induced by earthquakes, and thereby resist diagonal shear cracks,
2. they hold together the vertical bar and prevent them from excessively bending outwards (in technical terms, this bending phenomenon is called buckling), and
3. they contain the concrete in the column. The ends of the ties must be bent at 135° hooks. Such hook ends prevent opening of hoops and consequently buckling of concrete and buckling of vertical bars.

ACI provisions for special moment resisting frames (SMRF)

Provision for Frame Beams

a. Basic Requirement: The basic requirements for Beams in SMRF according to section 21.3.1.1 are summarized as follows

1. Factored axial compression force ≤ Ag.f'c /10 (where, Ag = Cross sectional area of Beam & f'c = Compressive strength of concrete.)
2. Clear span ≥ (4 x Effective depth of beam)
3. Width-to-depth ratio ≥ 0.3
4. Beam Width ≥ 10 in.
5. Beam Width ≤ Width of the supporting member (measured on perpendicular plan to the beam longitudinal axis of beam) + Distance on each side of supporting member not exceeding three-forth depth of the Beam)

b. Flexural Reinforcement

1. Minimum Reinforcement ratio, ρ ≥ 3√f'c/fy and 200/fy
2. Maximum Reinforcement ratio, ρ ≤ 0.0025
3. At least two reinforcing bars top and bottom must be provided continuously throughout the member.
4. The positive moment capacity at the face of columns must be at least one-half of the negative moment strength at the same location.
5. Neither positive nor negative moment strength at any section in a member may be less than one-fourth of the maximum moment strength at either end of the member.

c. Lap splices

1. Not within the joints
2. Not within twice the member depth; 2h, from the face of a joint or at other locations where flexural yielding is expected.
3. Lap splices must be enclosed by hoops or spirals with a maximum spacing of one-fourth of the effective depth or 4 in.
4. welding and mechanical connections are allowed provided they are not used in the locations as specified under 2.

d. Transverse reinforcement

I. Transverse reinforcement in the form of hoops must be used over a length equal to twice the member depth measured from the face of the supporting member toward midspan at both ends, as per calculation, but fulfilling following conditions.

1. The first hoops must be located not more than 2 in from the face of the supporting member.
2. Max spacing of the hoops over the length must not exceed:
   1. ¼ of d of beam,
   2. 8 times dia of smallest longitudinal steel,
   3. 24 dia of hoop bar
   4. or 12 in.

II. Elsewhere hoops as per calculation but spacing not to exceed d/2

Provision for Columns

A. Size

1. Each side at least 12 in
2. Shorter to longer side ratio ≥ 0.4. i.e. 12/12, 12/18, 12/24 OK; but 12/36 not O.K

B. Flexural reinforcement

C. Lap splices

1. Within the middle half as shown
2. Tie spacing at lap splice is d/4 or 4 inch, whichever is less

where d is effecive depth along least dimension of col.

Lap splice length = 1.3 ld = 1.3x 0.05 fy/ √ fc 50 db for fc 3 and fy 40 ksi 70 db for fc 3 and fy 60 ksi

D. Transverse Reinforcement

1. ACI Code 21.4.4 specifies the use of minimum transverse reinforcement over length Lo from each joint face. The length Lo may not be less than
   1. the depth "d" of the member at the joint face or at the section where flexural yielding is likely to occur
   2. one-sixth of the clear span of the member; hc/6 or
   3. 18 in.
2. Max spacing of ties within length Lo
   1. Least lateral dimension of col /4
   2. 6 db of longitudinal bar in col
   3. 4 + (14 - hx) /3 ; but not more than 6 inch and not less than 4 inch.
3. Elsewhere spacing of ties is least of 6 db or 6 inch.

Weak beam-Strong Column design :

For a frame the flexural capacity) of the members at a joint should be such that the columns are stronger than the beams. In this way. hinges will form in the beams rather than the columns, maintaining the overall vertical load capacity. For these reasons. the "weak beam-strong column" approach is used to design reinforced concrete frames subject to seismic loading.

Beam Column Joints

ACI recommendations: To provide adequate confinement within a joint, the transverse reinforcement used in columns must be continued through the joint. in accordance with ACI Code21.5.2.

• To provide adequate development of beam reinforcement passing through a joint, ACI Code 21.5.1 requires that the column dimension parallel to the beam reinforcement must be at least 20 times the diameter of the largest longitudinal bar.

• Beam longitudinal reinforcement that is terminated within a column. must be extended to the far face of the column core.

The development length of bars with 90° hooks must be not less than 8 db, 6 in., Or

ACI provisions for Intermediate moment resisting frames (IMRF)

Provision for Beams

1. Size: No special requirement (Just as ordinary beam requirement)
2. Flexural Reinforcement
   1. Min Steel as given in equation
   2. But need not be greater than 4/3 of that required by analysis.
   3. Min two reinforcing bars top and bottom, throughout the member.
   4. The positive moment capacity at the face of columns must be at least one-third of the negative moment strength at the same location.
   5. Neither positive nor negative moment strength at any section in a member may be less than one-fifth of the maximum moment strength at either end of the member.
3. Transverse Steel
4. Lap

Provision for Columns

1. Size: No special requirement (Just as ordinary Col requirement) 2. Flexural steel: No special requirement (Just as ordinary Col requirement) 3. Transverse steel: Less Stringent requirement as given next 4. Lap: No special requirement (Just as ordinary Col requirement)

For columns, within length L0 from the joint face, the tie spacing so may not exceed

• 8 times the diameter of the smallest longitudinal bar,

• 24 times the diameter of the tie bar,

• one-half of the smallest cross-sectional dimension of the column,

• or 12 in.,

in accordance with ACI Code 21.8.5.

Miscellaneous considerations

• IMRF are not allowed in regions of high seismic risk, however, SMRF are allowed in regions of moderate seismic risk.

• Unlike regions of high seismic risk, two way slab system without beams are allowed in regions of moderate seismic risk.

• In regions of low or no seismic risk ordinary moment resisting frames OMRF are allowed but IMRF and SMRF may also be provided.