Estimation and Analysis of Missing Precipitation Data
- Estimation of Missing Precipitation Data
- Consistency of Precipitation Data or Double Mass Index
Methods for Estimation of Missing Rainfall Data
- Some precipitation stations may have short breaks in the records because of absence of the observer or because of instrumental failures. It is often necessary to estimate this missing record.
- In the procedure used by the U.S. Weather Bureau, the missing precipitation of a station is estimated from the observations of precipitation at some other stations as close to and as evenly spaced around the station with the missing record as possible.
- The station whose data is missing is called interpolation station and gauging stations whose data are used to calculate the missing station data are called index stations.
There are two methods for estimation of missing data.
- Arithmetic Mean Method
- Normal Ratio Method
1. Simple Arithmetic Mean Method
According to the arithmetic mean method the missing precipitation 'Px' is given as:
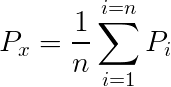
Where 'n' is the number of nearby stations, 'Pi' is precipitation at ith station and 'Px' is missing precipitation.
In case of three stations 1, 2 and 3,
Px = (P1 + P2 + P3)/3
Naming stations as A, B and C instead of 1, 2 and 3
Px = (Pa + Pb + Pc)/3
Where Pa , Pb and Pc are defined above.
2. Normal Ratio Method
According to the normal ratio method the missing precipitation is given as:
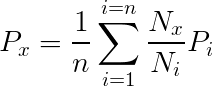
Where Px is the missing precipitation for any storm at the interpolation station 'x', Pi is the precipitation for the same period for the same storm at the "ith" station of a group of index stations, Nx the normal annual precipitation value for the 'x' station and Ni the normal annual precipitation value for 'ith' station.
For example, for the symbols defined above for three index stations in a catchment area. 
If the normal annual precipitation of the index stations lies within ±10% of normal annual precipitation of interpolation station then we apply arithmetic mean method to determine the missing precipitation record otherwise the normal ratio method is used for this purpose.
Consider that record is missing from a station 'X'.
Now let
N = Normal annual precipitation. (Mean of 30 years of annual precipitation data)
P = Storm Precipitation.
Let Px be the missing precipitation for station 'X' and Nx , the normal annual precipitation of this station, Na, Nb and Nc are normal annual precipitations of nearby three stations, A, B and C respectively while Pa, Pb and Pc are the storm precipitation of that period for these stations.
Now we have to compare Nx with Na , Nb and Nc separately. If difference of Nx - Na, Nx - Nb, Nx - Nc is within 10% of Nx then we use simple arithmetic mean method otherwise the normal ratio method is used.
Example
Find out the missing storm precipitation of station 'C' given in the following table:
|
Station |
A
|
B
|
C
|
D
|
E
|
| Storm precipitation (cm) |
9.7
|
8.3
|
----
|
11.7
|
8.0
|
| Normal Annual precipitation (cm) |
100.3
|
109.5
|
93.5
|
125.7
|
117.5
|
Solution
In this example the storm precipitation and normal annual precipitations at stations A, B, D and E are given and missing precipitation at station 'C' is to be calculated whose normal annual precipitation is known. We will determine first that whether arithmetic mean or normal ratio method is to be applied.
10% of Nc = 93.5 x 10/100 = 9.35
After the addition of 10% of Nc in Nc, we get 93.5 + 9.35 = 102.85
And by subtracting 10% we get a value of 84.15
So Na, Nb, Nd or Ne values are to be checked for the range 102.85 to 84.15.
If any value of Na, Nb, Nd or Ne lies beyond this range, then normal ratio method would be used. It is clear from data in table above that Nb, Nd and Ne values are out of this range so the normal ratio method is applicable here, according to which
Pc = (1/4)(93.5 x 9.7/100.3 + 93.5 x 8.3/109.5 + 93.5 x 11.7/125.7 + 93.5 x 8.0/117.5) = 7.8 cm
Example
Precipitation station "X" was inoperative for part of a month during which a storm occurred. The storm totals at three surrounding stations A, B and C were respectively 10.7, 8.9 and 12.2 cm. The normal annual precipitation amounts at stations X, A, B and C are respectively 97.8, 112, 93.5 and 119.9 cm. Estimate the storm precipitation for station 'X'.
Solution
Pa = 10.7 cm Na = 112 cm
Pb = 8.90 cm Nb = 93.5 cm
Pc = 12.2 cm Nc = 119.9 cm
Px = ? Nx = 97.8 cm
10% of Nx = 97.8 x 10/100 = 9.78 cm.
Nx - Na = 97.8 - 112 = -14.2 cm Þ More than + 10% of Nx (no need of calculating Nx - Nb and Nx - Nc
Px = (1/3)( 97.8x 10.7/112+ 97.8x 8.90 /93.5 + 97.8x 12.2 /119.9)
Px = 9.5 cm
Estimation of Missing Precipitation Data
This situation will arise if data for rain gauges are missing (e.g. due to instrument failure). Data from surrounding gauges are used to estimate the missing data. Three approaches are used:
Arithmetic mean:
Use when normal annual precipitation is within 10% of the gauge for which data are being reconstructed
Where:
Pm = precipitation at the missing location
Pi = precipitation at index station I
N = number of rain gauges
The Normal ratio method:
Normal ratio method (NRM) is used when the normal annual precipitation at any of the index station differs from that of the interpolation station by more than 10%. In this method, the precipitation amounts at the index stations are weighted by the ratios of their normal annual precipitation data in a relationship of the form:
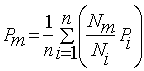
Where:
Pm = precipitation at the missing location
Pi = precipitation at index station
Nm = average annual rain at ‘missing data’ gauge
Ni = average annual rain at gauge
N = number of rain gauges
Reciprocal Inverse Weighting Factor Approach
Procedure:
- Divide area around gauge of interest into four quadrants
- Using records at nearest station in each quadrant
- Compute missing precipitation amount:
Where:
Pi = rainfall recorded by gauge i
Xi = distance from gauge i to missing data point
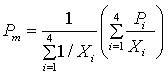
Consistency of Precipitation Data
A double-mass curve is used to check the consistency of a rain gauge record:
- compute cumulative rainfall amounts for suspect gauge and check gauges
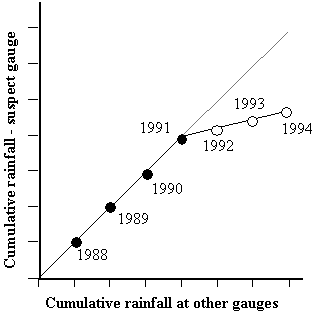
- plot cumulative rainfall amounts against each other (divergence from a straight line indicates error)
- multiplying erroneous data after change by a correction factor k where
Missing Rainfall Data Video
Precipitation Analysis
- Areal precipitation estimation
- Depth-area analysis
- Precipitation frequency
- Intensity-duration analysis
- Intensity-duration- frequency analysis
Areal Precipitation Estimation
- Arithmetic mean method
- Thiessen method
- Isohyetal method
Arithmetic mean method
Theissen Method
- Divide the region (area A) into sub-regions centred about each rain gauge;

- Determine the area of each sub-region (Ai) and compute sub-region weightings (Wi) using: Wi = Ai/A
- Compute total aerial rainfall using
Isohyetal Method
Potentially most accurate approach, but subjective
- Plot gauge locations on a map;
- Subjectively interpolate between rain amounts between gauges at a selected interval;
- Connect points of equal rain depth to produce lines of equal rainfall amounts (isohyets);
- Compute aerial rain using:
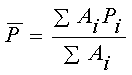
Infiltration Indexes
- Infiltration index is the average rate of loss such that the volume of rainfall in excess of that rate will be equal to direct runoff.
- Estimates of runoff volume from large areas, having heterogeneous infiltration and rainfall characteristics, are made by use of infiltration indexes.
- Infiltration indexes assume that infiltration rate is constant throughout the storm duration. This assumption tends to underestimate the higher initial rate of infiltration while overestimating the lower final rate.
- Infiltration indexes are best suited for applications involving either long-duration storms or a catchment with high initial moisture content. Under such conditions, the neglect of the variation of infiltration rate with time generally justified on practical grounds.
- Two types of indexes: Phi-index and W-index are used.
Hydrologic Soil groups
All soils are classified into four hydrologic soil groups of distinct runoff-producing properties. These groups are labeled A, B, C and D. Following is the brief of their runoff and infiltration properties:
A Lowest runoff potential (Greater than0.03 in/hr)
B Moderately low runoff potential (0.15 – 0.30 in/hr)
C Moderately high runoff potential (0.05 – 0.15 in/hr)
D Highest runoff potential (0 – 0.05 in/hr)
Land use and Treatment
- The effect of the surface conditions of a watershed is evaluated by means of land use and treatment classes.
- Land use belongs to watershed cover, including every kind of vegetation, litter and mulch, fallow (bare soil), as well as nonagricultural uses such as water surfaces (lakes, swamps), impervious surfaces (roads, roof, and the like), and urban areas.
- Land treatment applies mainly to agricultural land uses, and it includes mechanical practices such as contouring or terracing and management practices such as grazing control and crop rotation.
- A class of land use/treatment is a combination often found in a literature.
Ground surface (Hydrologic) condition
Hydrologic condition is based on combination of factors that affect infiltration and runoff, including:
- Density and canopy of vegetative areas,
- Amount of year-round cover,
- Amount of grass or close-seed legumes in rotations,
- Percent of residue cover on the land surface
- Degree of roughness
Poor: Factors impair infiltration and tend to increase runoff
Good: Factors encourage average and better than average infiltration and tend to decrease runoff.