Bligh's Creep Theory for Hydraulic Structures
Design of impervious floor for sub surface flow: It is directly depended on the possibilities of percolation in porous soil on which the floor (apron) is built. Water from upstream percolates and creeps (or travel) slowly through weir base and the subsoil below it. The head lost by the creeping water is proportional to the distance it travels (creep length) along the base of the weir profile. The creep length must be made as big as possible so as to prevent the piping action. This can be achieved by providing deep vertical cut-offs or sheet piles.
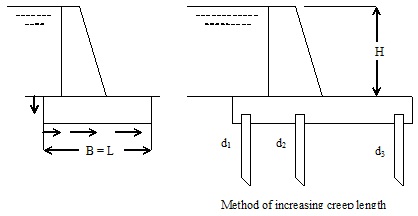
According to Bligh’s theory, the total creep length for first drawing: L = B and for second drawing: L = B + 2(d1 + d2 + d3)
If H is the total loss of head, then the loss of head per unit length of the creep shall be
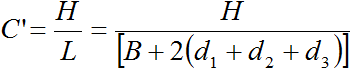
Bligh called the loss of head per unit length of creep as Percolation coefficient. The reciprocal, (L/H) of the percolation coefficient is known as the coefficient of creep C.
Assumptions
- Hydraulic slope or gradient is constant throughout the impervious length of the apron.
- The percolating water creep along the contact of the base profile of the apron with the sub soil losing head en-route, proportional to length of its travel. The length is called creep length. It is the sum of horizontal and vertical creep.
- Stoppage of percolation by cut off (pile) possible only if it extends up to impermeable soil strata.
Design criteria:
Safety against piping:
The creep length should be sufficient to provide the safe hydraulic gradient according to the type of soil. According to the Bligh's Creep Theory if H ≤1C then there will be no danger of piping. The length of creep should be sufficient to provide safe hydraulic gradient according to the type of soil. The values of Bligh’s coefficient C for different type of soils as suggested by Bligh’s are:
Safe creep length = L = CH, C = 1/c
Safety against uplift pressure:
Let h' = uplift pressure head at any point of apron (Hydraulic gradient line above the bottom of floor)
The uplift pressure = wh' where w = density of water. If t = thickness of floor at the point, l = specific gravity for floor material. Then, downward force per area (resisting force) = t.w.e or wh' = t.w.e
For portion of floor upstream of barrier only nominal thickness need to be provided since the weight of water will counterbalance the uplift pressure. A certain minimum length of impervious floor is always necessary to the downstream of the barrier (thickness of downstream floor for worst condition)
Limitations of Bligh's Creep Theory
- This theory made no distinction between horizontal and vertical creep.
- Did not explain the idea of exit gradient - safety against undermining cannot simply be obtained by considering a flat average gradient but by keeping this gradient will be low critical.
- No distinction between outer and inner faces of sheet piles or the intermediate sheet piles, whereas from investigation it is clear, that the outer faces of the end sheet piles are much more effective than inner ones.
- Losses of head does not take place in the same proportions as the creep length. Also the uplift pressure distribution is not linear but follow a sine curve.
- In case of two piles the width between should be greater than twice the head or the piles are not effective.