General Stability Criteria of Weirs

Stability analysis have been carried out for structures for most severe conditions of horizontal and vertical forces. Stability criteria are aimed at ensuring the overall safety of structure against overturning, flotation and sliding.
Overturning
The structures have been designed so that it should be safe against overturning at any horizontal plane within the structure at the base, or at a plane below the base. The overturning stability have been calculated by applying all the vertical forces (SV) and lateral forces for each loading condition to the structure and, then, summing moments (SM) caused by the consequent forces about the downstream toe. The resultant location (RL) along the base is given as: -
Resultant Location (e)
RL = Σ M / Σ V
Allowable limits under different loading conditions are as follows:
Normal Loading
Resultant of all forces acting on structures will fall within the middle sixth of the base (i.e. no tension allowed between concrete and foundation) and the allowable foundation pressure will not be exceeded.
Exceptional loading
Resultant of all forces acting on the structure will remain within the middle third of the base and allowable design foundation pressure (20% higher than for Normal loading case) will not be exceeded.
Extreme loading
Resultant of all forces acting on the structure will remain within the middle half of the base provided that a minimum of 75% of the base area is subject to compression and the maximum base pressure will not exceed the allowable design foundation pressure (33% higher than for Normal loading case).

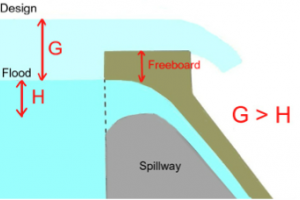
Typical Example of Weir
Sliding
The structure have been designed so that it should be safe against sliding on any horizontal or near-horizontal plane within the structure at the base or on any rock seam in the foundation. Sliding stability has been checked with the following equation:
Force causing sliding = Pn
Where Pn = Σ Horizontal forces
Force resisting sliding = f (W + Pv)
Where f = Co-efficient of function between soil & concrete
W = Total weight
Pv = Σ vertical forces
The minimum factors of safety for the project are as follows: -
Loading ConditionFactor of Safety
Normal loading 1.50
Exceptional loading 1.25
Extreme loading 1.10
Where
- Normal Loading
Resultant of all forces acting on structures will fall within the middle sixth of the base (i.e. no tension allowed between concrete and foundation) and the allowable foundation pressure will not be exceeded.
- Exceptional loading
Resultant of all forces acting on the structure will remain within the middle third of the base and allowable design foundation pressure (20% higher than for Normal loading case) will not be exceeded.
- Extreme loading
Resultant of all forces acting on the structure will remain within the middle half of the base provided that a minimum of 75% of the base area is subject to compression and the maximum base pressure will not exceed the allowable design foundation pressure (33% higher than for Normal loading case). For concrete structures on weak foundations, it is usually not feasible to obtain safety factors equivalent to those prescribed for structures on competent rock. It has been common practice to relax the factor of safety for concrete structures on non-rock/weak rock foundations. The factor of safety is established on the basis of results of site investigation and judgment of experienced designers.
Flotation
An empty tank constructed in water bearing soil will tend to move upwards, in the ground or float. This affect was also considered into account in design of hydraulic structures. Specially in the design of weir apron on d/s side. Safety against flotation of concrete structures has been checked with the following equation:
Factor of safety = ( Σ V - U) / U
Where
Σ V = downward vertical forces
U = uplift force
The minimum factors of safety against flotation in different conditions are as follows: -
LOADING FACTOR OF SAFETY
Normal Loading 1.25
Exceptional Loading 1.15
Extreme Loading 1.05
BEARING PRESSURE
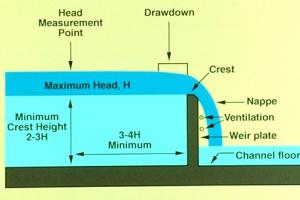
The following equation has been used to compute the bearing pressure at critical locations on the foundation:
Where,
Fb = Bearing pressure
Σv = sum of all vertical loads
A = Area of the base
Σ M = sum of all the moments about the center of the base
Y = distance from the center of gravity of the base to the location where the bearing pressure is to be computed
I = Moment of Inertial of the base